|
The Hour Record at Altitude
It is well known that the air density decreases with an increase in
altitude,
which reduces the aerodynamic drag but also reduces the athletes power
output. In a recent paper by P. D. Heil the author gives a nice overview about
this topic, for details look
at his paper at:
Heil,
D. P. European Journal of Applied Physiology, Vol.
93, 5-6, 547 - 554
|
The density of air varies with barometric pressure and
temperature, both of
which decrease with an increase in altitude (Olds et al. 1995b).
r = 1.225 ×
(PB / 760) × (288.15/T)
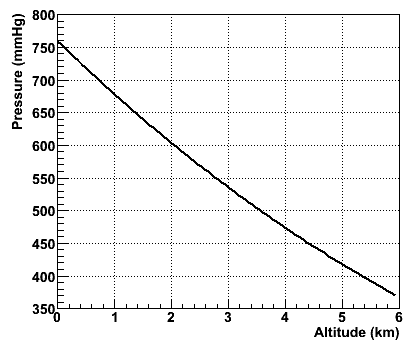
The pressure PB follows the well known "barometric altitude
equation":
PB=exp(6.63268-0.112 × H -
0.00149 × H2)
where PB is the barometric pressure in mmHg and H is the altitude in
km (West 1996), which is shown in the figure on the right. If we assume
that cycling records will be attempted at a temperature around
20 o C, the air density is just a function fo the altitude:
So it is obvious to go as high as possible, isn't it? |
 |
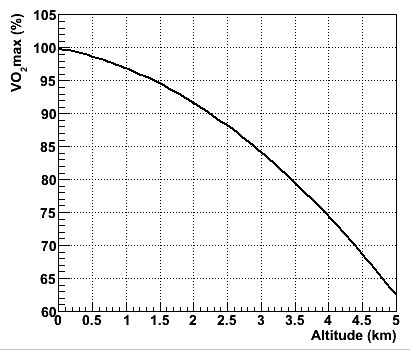
| It's not so easy, since the
athlete's ability to consume oxygen is comprised with an increase in
altitude:
KA = 99.921 - 1.8991*H - 1.1219*H²
where KA is the VO2max expressed as a percentage of
VO2max
at sea level (Basset et al. 1999), see figure on the right. So for example at 4
km altitude the athletes VO2max has decreased to about 75% compared to sea
level.
|
 |
| |
|
|
Now we just have to modify our basic equations from
the
motion of a cyclist
page:
PAir = FAir×v
= 0.5 ×cwA×r×v³
with different values for r at different
altitudes,
the power output of the athlete PRider has to be
reduced in parallel.
The result is the predicted hour record as a function of the altitude. The
effect is
clearly to see: If one takes Boardman's hour record at sea level of ca. 56,375 km/h, with
increasing altitude
the speed increases more an more, until a maximum of about 59,4 km/h is reached
for an altitude of about 3200 m. At higher altitudes the velocity decreases
again.
Similar results (optimal altitude around 3000 m - 3500 m) were found also by
other
authors. So in principle the velodrome in La Paz (Bolivia) at 3400 m should be
perfect.
Its interesting that the Mexico City velodrome at 2230 m should already give an
advantage of
about 2,5 km/h !
For the UCI hour record with standard bikes the results are comparable, Chris Boardman's attempt of 49.4 km/h
would be around 51,7 km/h at Mexico City. So, comparing Eddy Merckx at Mexico City and Chris Boardman or Ondrej Sosenka at sea
level, this makes their records even more impressive. |
|
|
References:
Heil,
D. P. European Journal of Applied Physiology, Vol.
93, 5-6, 547 - 554
Basset et al. 1999: Med Sci Sports Exerc 31:1665-1676
Olds et al. 1995: J Appl Physiol 78:1596-1611
West 1996: J Apll Physiol 81:1850-1854
|
|