|
Der Stundenweltrekord in der Höhe
Wie bekannt ist, verringert sich die Luftdichte mit zunehmender Höhe,
wodurch der Luftwiderstand sinkt, gleichzeitig verringert sich aber auch
die
Leistung, die der Athlet erbringen kann. In einer neuen
Veröffentlichung (in
Englisch)
von P. D. Heil gibt der Autor einen überblick über dieses Thema,
für Details
siehe hier:
Heil,
D. P. European Journal of Applied Physiology, Vol.
93, 5-6, 547 - 554
|
Die Dichte der Luft schwankt mit Luftdruck und Temperatur,
beide verringern sich mit zunehmender Höhe (Olds et al. 1995b):
r = 1.225 ×
(PB / 760) × (288.15/T)
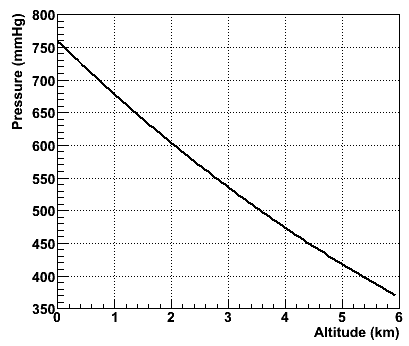
Der Druck PB folgt der bekannten "barometrischen
Höhenformel":
PB=exp(6.63268-0.112 × H -
0.00149 × H2)
wobei PB der Luftdruck in mm Hg ist und H die Höhe in Kilometer
(West 1996), siehe Abbildung rechts.
Wenn wir der Einfachheit halber annehmen, dass ein Weltrekordversuch bei einer
Temperatur um 20o C versucht werden wird, ist die Luftdichte nur eine
Funktion
der
Höhe. Je weniger Luftdichte, desto weniger Luftwiderstand, und deshalb
eine höhere Geschwindigkeit. Also sollte man so hoch gehen wie nur irgend möglich, ganz
einfach,
oder? |
 |
Es ist leider nicht so einfach, da in der dünneren
Luft auch weniger Sauerstoff enthalten ist, der Athlet also auch weniger
Leistung erbringen kann als auf Meereshöhe. Die nachfolgende Formel gibt an,
wie
sich der Wert für VO2max (ein Wert, der
Leistungsfähigkeit eines
Athleten beschreibt) mit der Höhe verändert
(Basset et al. 1999):
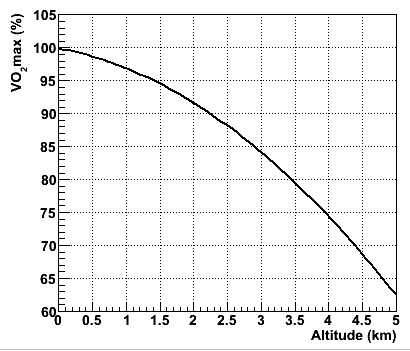
KA = 99.921 - 1.8991*H - 1.1219*H²
wobei KA das Verhältnis von VO2max in der
Höhe zum VO2max am Meeresspiegel
ausdrückt,
siehe Abbildung rechts. So hat zum Beispiel in vier Kilometern
Höhe der
Athlet nur noch etwa 70% der Leistung auf Meereshöhe. |
 |
| |
|
|
Jetzt müssen wir nur unsere Gleichung von der Seite "Leistung beim Radfahren"
ändern:
PAir = FAir×v
= 0.5 ×cwA×r×v³
mit unterschiedlichen Werten für r für
unterschiedlichen Höhen, zugleich muss die Abgabeleistung des
Athleten
P
Rider
in der entsprechenden Formel verringert werden. Als Resultat
erhält man den Stundenweltrekord als Funktion der Höhe. Der Effekt ist
offensichtlich: Wenn man einen Stundenweltrekord auf Meereshöhe von 56,4
km/h annimmt, erhöht sich mit zunehmender Höhe die Geschwindigkeit immer
mehr, bis ein Maximum von ungefähr 59,4 km/h bei einer Höhe von
ungefähr
3200 m erreicht wird. Bei noch größeren Höhen verringert sich die
Geschwindigkeit wieder.
Ähnliche Resultate (optimale Höhe um 3000 m - 3500 m) wurden auch
von
anderen Autoren publiziert. Im Prinzip sollte also das Velodrom von La Paz
(Bolivien) auf 3400 m Höhe optimal sein. Interessant ist, dass
die Bahn
von
Mexiko-City auf 2230 m schon einen Vorteil von ungefähr 2,5 km/h
geben sollte!
Für den UCI Stundenweltrekord für Standard-Fahrräder sind die Resultate vergleichbar, so
würde der
Rekord 49.4 km/h, auf Meereshöhe aufgestellt, etwa bei 51,7 km/h in
Mexiko-City oder sogar
bei etwa 52 km/h auf 3200 m liegen! Vergleicht man also den Rekord von Eddy Merckx
in Mexico-City und Chris Boardmans oder Ondrej Sosenkas Rekord, so werden diese Leistungen
noch eindrucksvoller. |
|
|
References:
Heil,
D. P. European Journal of Applied Physiology, Vol.
93, 5-6, 547 - 554
Basset et al. 1999: Med Sci Sports Exerc 31:1665-1676
Olds et al. 1995: J Appl Physiol 78:1596-1611
West 1996: J Apll Physiol 81:1850-1854 |
|